|
1. Difração através de uma fenda
1.1 Diagrama
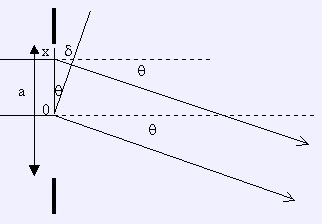
1.2 Intensidade da luz no infinito
a = 2R
Em x, o desfasamento em relação a 0, δ = x sen θ = x θ
(θ é pequeno)
φ
= 2 π δ/λ =
2πθ/λ x
|
A amplitude das ondas difratadas no infinito é A = A0 |
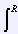 |
-R
e-j φ
dx
= A0 |
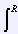 |
-R cos
φ
dx - j a0 |
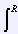 |
-R
sen
φ
dx |
|
o termo em sen dá 0, logo: A = A0 |
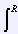 |
-R cos
(2πθ/λ
x) dx = 2A0 sen
(2πθ /λ
R)/(2πθ /λ)
|
A = 2RA0 sen
(πaθ /λ)/(πaθ /λ)
I = A2 = a2A02 sen2
(πaθ /λ)/(πaθ /λ)2
I = Im sen2
(π aθ /λ)/(π aθ
/λ)2
1.3 Franjas escuras
Os zeros correspondem a sen2
(π aθ /λ)
= 0 logo, se π a θ /λ
= k π
θ /λ
= k/a
θ
= k λ/a
2. Difração através de uma fenda circular
2.1 Diagramas
2.2 Intensidade da luz no infinito
a = 2R
Em x, o desfasamento em relação a 0, δ = x sen θ = x θ
(θ é pequeno)
φ
= 2πδ/λ =
2πθ/λ
x
A amplitude Ax emitida por um elemento da superfície da fenda circular é A0
2ydx
e-j φ
y = (R2
-x2)1/2
logo: Ax = 2A0(R2
-x2)1/2 e-j
φ dx
|
A amplitude das ondas difratadas no infinito é A = 2A0 |
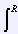 |
-R
(R2
- x2)1/2 e-j
φ dx |
|
A = 2A0 |
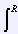 |
-R (R2
- x2)1/2 cos
φ
dx + j 2A0 |
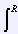 |
-R
(R2
- x2)1/2sen
φ
dx |
|
o termo em sen dá 0, logo: A = 2A0 |
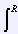 |
-R (R2
-x2)1/2 cos
(2πθ /λ
x) dx |
|
A = 4A0 |
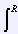 |
0 (R2
- x2)1/2 cos
(2πθ /λ
x) dx |
| Mudando de variável u = x/R, então A = 4A0R2 |
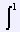 |
0 (1
- u2)1/2 cos
(2πRθ /λ
u) du |
|
A = 4A0R2 |
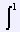 |
0 (1
- u2)1/2 cos
(πaθ /λ
u) du |
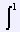 |
0 (1
- u2)1/2 cos
(πaθ /λ
u) du = π/2
J1(πaθ /λ)/(πaθ /λ)
J1(x) é a função de Bessel |
J1(x) = x/2 S (-1)n
(x/2)2n /((n+1)
n!2)
A = 2πA0R2
J1(πaθ /λ)
/ (πaθ /λ)
I = A2 = π2A02a4 /2
J12(πaθ /λ)/(πaθ /λ)2
I = Im
J12(πaθ
/λ)/(πaθ
/λ)2
2.3 Franjas escuras
Os zeros correspondem a J12(πaθ /λ)
= 0, o que corresponde a:
θ a/l
= 1,22 ; 2,23 ; 3,24 ; 4,24 ; 5,24 ; 6,24 ; 7,24 ; 8,25 .........
3. Poder de resolução de um instrumento de ótica
3.1 Diagrama
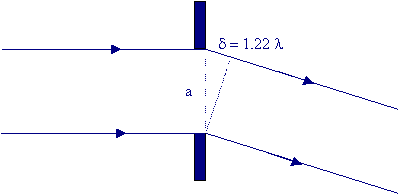 |
O primeiro zero encontra-se para θ
= 1,22 λ/a
, ou seja, quando o raio que passa pelo topo da abertura faz um trajeto mais longo em 1,22
λ que o raio que passa pela parte inferior.
Na prática, o poder de resolução acaba por ser uma noção aproximada, podendo-se ter uma
diferença de λ. |
3.2 Critério de Rayleigh
Considera-se que dois pontos são discerníveis se as suas imagens, dilatadas
pela difração devida à objetiva do instrumento ótico, são tais que o mínimo de uma é confundido com o máximo da outra.
Tem-se então:
A origina uma imagem centrada em B e A' origina uma imagem B', portanto o
primeiro mínimo de difração está também em B.
Estes dois pontos, A e A ', são considerados discerníveis (critério de Rayleigh)
Se se considerar AA' = d e α o ângulo a partir
do qual o objetivo se vê depois do ponto A, então a diferença de movimento δ
entre os dois raios extremos (a vermelho) vale:
δ = (( D/2 +d )² + L²)1/2 - (( D/2 - d )² + L²)1/2 =
( D²/4 + L² + Dd )1/2 - ( D²/4 + L² - Dd )1/2 negligenciando d²
δ = ( D²/4 + L² )1/2((1 + Dd/( D²/4 + L²))1/2 -
(1 - Dd/( D²/4 + L²))1/2 = ( D²/4 + L²)1/2(1 + 0,5 Dd/( D²/4 + L² ) - 1
- 0,5 Dd/(D²/4 + L²)
δ = ( D²/4 + L²)1/2(Dd/( D²/4 + L² ) = Dd/( D²/4 + L² )
1/2 ou D/( D²/4 + L² )1/2 =
2d sen(α/2)
δ =
2d sen(α/2)
Logo, pelo critério de Rayleigh, os dois pontos serão discerníveis se 2d sen(α/2)
= λ
d = λ/(2 sen(α/2))
α não é muito grande, logo: 2sen(α/2)
= sen α
d = λ/ senα
3.3 Poder de resolução de um telescópio espacial
No espaço, a resolução real de um telescópio não se vê reduzida pelas
turbulências, como ocorre nos telescópios terrestres de ótica não adaptativa.
θ = d /L = λ/(L senα)
α é muito pequeno, logo: L senα
= L α = D
θ = λ/(L senα) = λ/D
θ = λ/D
O telescópio Hubble tem um diâmetro de 2,4 m. Considerando um λ
médio de 500 nm, obtém-se θ = 2,1.10-7 rd, o que corresponde a distinguir uma cratera de
80 m de diâmetro na lua.
3.4 Poder de resolução de um microscópio
d = λ/(2
sen(α/2))
α é próximo de 60°, portanto com um microscópio não se pode distinguir um detalhe mais pequeno que λ,
que está na ordem de 1µm.
Nota: Pode-se aumentar a resolução diminuindo λ,
o que se pode conseguir imergindo a objetiva e a preparação num líquido com um forte índice de refração (n).
Tem-se então λ = c/(nf) =
λ0 /n e d é dividido por n. É por esta razão
que existem as objetivas ditas "de imersão".
Traduzido e adaptado
para a Casa das Ciências por Diana Barbosa e Manuel Silva Pinto em Setembro de 2011

|