A refração               

1. Diagramas

Os índices n₁ e n₂ dos dois meios 1 e 2 são idênticos, de acordo com velocidade da luz em vácuo e com a velocidade da luz no meio.
n₁ = c/c₁  e    n₂ = c/c₂.

2. Lei de Snell-Descartes

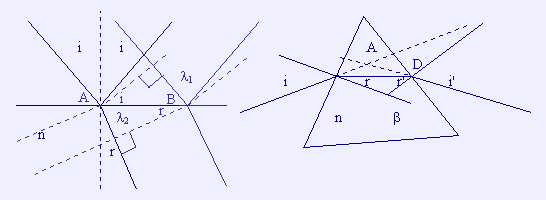
λ₁ = AB sen i, logo AB = λ₁/sen i
λ₂ = AB sen r, logo AB = λ₂/sen r

Logo λ₁/sen i = λ₂/sen r.   λ₁ = c₁/f,   λ₂ = c₂/f  (c₁ e c₂ são as velocidades da luz em cada meio e f é a frequência da luz).

Obtém-se: c₁/sen i = c₂/sen r   ou   sen i /c₁ = sen r /c₂.

Tem-se n₁ = c/c₁  e   n₂ = c/c₂, logo tem-se:  n₁ sen i  = n₂ sen r

    n₁ sen i = n₂ sen r

3. O prisma

3.1 Ângulo de saída do raio

Tem-se n₁ = 1 e n₂ = n  (n é o índice do vidro de que é feito o prisma).

Então: sen i = n sen r
β = 360 - 2x90 - A = 180 - A
r + r' + β =180 => r + r'  =180 - β =  A
r' =  A -  r
sen i' = n sen r'

3.2 Ângulo de desvio (D)

D = i - r + ( i' - r' ) =  i  +  i' - A

   D = i  +  i' - A

D passa por um mínimo (D_m) quando r = r'. Logo, quando i = i'
r = r' = A/2 => sen i_m = sen i'_m = n sen A/2

D = D_m  si  i_m =  i'_m =  arcsen( n sen A/2 )

   D_m  =  2 i_m - A

3.3 Intensidades refletidas

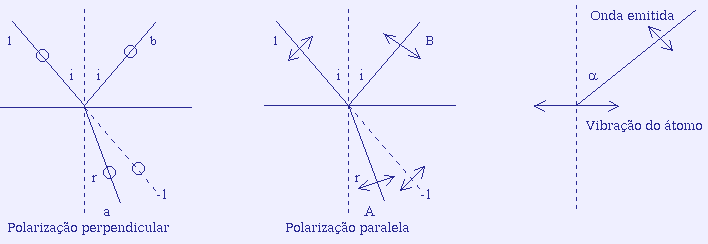
A luz refratada faz vibrar os átomos do "vidro" e estas vibrações criam ondas de interferência. O resultado destas interferências é a onda refletida e uma onda em oposição de fase com a onda incidente que atravessa o vidro e que origina uma amplitude total nula nessa direção (linha em pontilhado).
Para a polarização perpendicular, a onda emitida pela vibração de um átomo é proporcional à amplitude dessa vibração.
Para a polarização paralela, a onda emitida pela vibração de um átomo é proporcional à amplitude dessa vibração e ao cosseno do ângulo α entre a perpendicular à vibração e a direção da onda emitida.

Produção da onda refletida: b = k a e B = k A cos( i + r ), logo: b/a = B/(A cos( i + r ))
Produção da onda de oposição: -1 = k' a e -1 = k' A cos( i - r ), logo: a = A cos( i - r )
Então: B/b = A cos( i + r )/a = cos( i + r )/cos( i - r )

Conservação da energia: 1 = a² + b² e 1 = A² + B²
(1 - B²)/(1 - b²) = A²/a² = 1/cos²(i - r )
(1-b²cos²( i + r )/cos²( i - r ))/(1 - b²)  = 1/cos²(i - r )

Resolvendo esta equação em b², obtém-se:
b² = sen²( i - r )/sen²( i + r )
e B² = b² cos²( i + r )/²cos( i - r ) = tan²( i - r )/tan²( i + r )

b² é a razão entre as intensidades refletidas e incidentes na componente perpendicular do campo, logo a componente perpendicular no plano de incidência:  
           Ir/I = sen²( i-r )/sen²( i+r )  (componente perpendicular no plano de incidência)

B² é a razão entre as intensidades refletidas e incidentes na componente paralela do campo, logo a componente paralela no plano de incidência:  
          Ir/I = tan²( i-r )/tan²( i+r )  (componente paralela no plano de incidência)

Caso particular da incidência perpendicular: i = r = 0
i e r baixos, sen i = i, tan i = i, sen r = r, tan r = r e  i = n r
Ir/I = (n r -r )²/( nr + r )²
         Ir/I = ( n-1)²/( n+1)²

Ângulo de Brewster

Se  i + r = 90°, a componente paralela Ir = 0, o que corresponde ao ângulo de Brewster i_B
sen i_B = n sen (90-i_B) = n cos i_B, logo: tan i_B = n

    i_B = arctan n

4. A reflexão total

Se n₂ > n₁, a luz é sempre transmitida (refratada) do meio 1 para o meio 2. Mas, se n₂ <  n₁, então depende do ângulo de incidência (i). Na verdade, tem-se sen r = n₁/n₂ sen i > sen i, ou sen r < = 1 como todo o bom seno, então não pode ocorrer refração senão se n₁/n₂ sen i < = 1 => sen i < = n₂/n₁. Existe então um ângulo limite i_L = arcsen(n₂/n₁), além do qual não há transmissão de luz, já que ela é inteiramente refletida na superfície de separação. Este é o fenómeno de reflexão total.

    Se  i > arcsen(n₂/n₁), dá-se a reflexão total na superfície de separação. 

Nota: A teoria eletromagnética da refração da luz a partir das equações de Maxwell, põe em evidência a existência de uma onda efémera no interior do meio 2. Esta onda decresce exponencialmente com a distância à superfície de separação e desaparece a uma distância de qualquer comprimento de onda. Ela é portanto muito difícil de visualizar com a luz visível (λ ~ 0,5 µm). Pelo contrário, é muito fácil de detetar com ondas de rádio refratadas através dum prisma de parafina.

5. Princípio de Fermat

Fermat afirma que o tempo de percurso da luz entre dois pontos é mínimo. (Para ser mais preciso, inferior a todo o percurso vizinho). Este principio permite redescobrir a lei de Snell-Descartes.

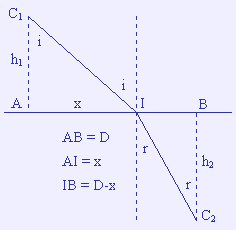O tempo de percurso entre C1 e C2:    t = C1I /c1 + C2I /c2 C1I = ( h12 + x2 )1/2  et  C2I = ( h12 + (D-x)2 )1/2 t = ( h12 + x2 )1/2 /c1 +  ( h12 + (D-x)2 )1/2 /c2 t é mínimo se dt/dx = 0 dt/dx = x/(c1 (h12 + x2 )1/2 )  - (D - x )/(c2 ( h12 + (D-x)2 )1/2)  = 0 mas x/(h12 + x2 )1/2  =  sen i   e   ( D - x )/( h12 + (D-x)2 )1/2  =  sen r Logo: sen i / c1 = sen r / c2 , o que é uma formulação da lei de Snell-Descartes. c/c1 = n1  et c/ c2  = n2 , logo         n1 sen i = n2 sen r

     Traduzido e adaptado para a Casa das Ciências por Diana Barbosa e Manuel Silva Pinto em Setembro de 2011