|
1. Princípio da teoria de Arrhenius
Consideremos uma reação simples entre duas espécies químicas A e B, que se transformam
em duas outras espécies C e D. Se a reação está em equilíbrio, a reação inversa também ocorre.
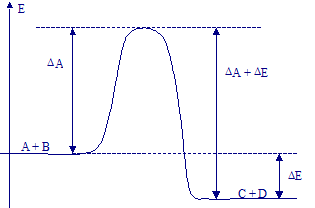
Estas reações dão-se por colisão entre as moléculas, se a energia das moléculas que colidem for igual ou superior a um certo limite ΔA
(energia de ativação) e se a disposição (orientação) respetiva das duas espécies for a correta.
A energia da reação entre A e B é ΔE
 |
N - número de moléculas por L
NA, NB
- número de moléculas A e B por L
Na - número de Avogadro
nA, nB
- número de moles A e B por L
σ - secção transversal da reação
τ - tempo médio entre duas colisões
vm - velocidade média das moléculas
l = 1/(Nσ ) = vm τ - livre percurso médio
Vs - Volume da mistura
x - avanço da reação |
2. Definição da velocidade
v = d(x/VS)/dt
A velocidade da reação é proporcional à probabilidade de reação entre A e B,
probabilidade esta que depende da quantidade de moles por unidade de volume nA, nB
v = k1 nAnB (k1
é a constante de velocidade da reação entre A e B)
3. Constante de velocidade
A velocidade da reação entre A e B é igual ao número de reações por segundo
por unidade de volume. Este número corresponde ao número de colisões multiplicado pela probabilidade de que a colisão origine uma reação.
Esta probabilidade é o produto da probabilidade de que a colisão se dê entre A e B e da probabilidade dessa colisão originar uma reação.
Esta probabilidade é, por sua vez, o produto da probabilidade de que a energia da colisão seja superior a ΔA
e que o arranjo das moléculas seja o correto.
Número de reações por segundo:
N/τ (τ é o tempo médio entre duas colisões e N/τ é, portanto, o número de colisões por segundo.)
Probabilidade de que a colisão se dê entre A e B : NA/N NB/N
Probabilidade de que a energia da colisão seja superior a ΔA
: e-ΔA/kT (fórmula de Boltzmann)
Probabilidade de que o arranjo das moléculas seja o correto : ζAB
Na v = ζAB e-ΔA/kT
NA/N NB/N
N/τ = ζAB
/(Nτ) e-ΔA/kT
NANB = ζAB
σAB
vm Na² e-ΔA/kT
nAnB
1/2 m vm² = 3/2 kT portanto vm
= (3 kT/m)1/2 (m
massa média dos dois reagentes (e dos dois produtos))
k1 = ζAB
σAB
Na (3 kT/m)1/2 e-ΔA/kT
O mesmo se passa para a reação inversa entre C e D: k2 = ζCD
σCD Na (3 kT/m)1/2 e-(ΔA
+ ΔE)/kT
4. Constante de equilíbrio da reação K
Para uma reação em equilíbrio v
= k1
nAnB - k2 nCnD
Em equilíbrio a velocidade é nula, portanto k1
nAnB = k2 nCnD
Por definição, K = nCnD/nAnB
portanto
K = k1/k2 = ζAB
σAB
(3 kT/m)1/2 e-ΔA/kT
/( ζCD
σCD (3 kT/m)1/2 e-(ΔA
+ ΔE)/kT ) = ζAB σAB/
( ζCD σCD )
e ΔE/kT
K = ζAB σAB/ (ζCD
σCD)
e ΔE/kT
Definimos ζAB σAB/ (ζCD
σCD) = Ki
Ki é a constante de equilíbrio apara T infinito
K = Ki
e ΔE/kT
Nas tabelas, as constantes de equilíbrio são indicadas para uma temperatura de 25 ºC (298 K : temperatura standard)
K25 = Ki e ΔE/(298k)
K = K25 e
(ΔE/kT - ΔE/(298k)
)
K = K25 e
ΔE/k (1/T - 1/298)
)
Numa reação exotérmica ( ΔE > 0 ) K
diminui com o aumento da temperatura, o que favorece a reação endotérmica inversa.
Numa reação endotérmica ( ΔE < 0 ) K aumenta se aumenta a temperatura,
o que favorece a reação endotérmica direta.
Numa reação atérmica ( ΔE = 0 ) o equilíbrio é independente da temperatura. É o caso da esterificação.
Isto está de acordo com as leis de limitação de Vant'Hoff-Le Chatellier.
5. Equação diferencial
| tempo |
A |
B |
C |
D |
| 0 |
n0A |
n0B |
0 |
0 |
| t |
n0A
- nC |
n0B
- nC |
nC |
nC |
v = d nC/dt = k1 nA
nB - k2 nC nD = k1
(n0A - nC ) ( n0B - nC ) - k2
nC² = k1 n0A n0B
- k1 ( n0A + n0B ) nC +
( k1 - k2 ) nC²
dnC/dt + k1
( n0A + n0B ) nC - ( k1 -
k2 ) nC² = k1 n0A
n0B
Solução numérica :
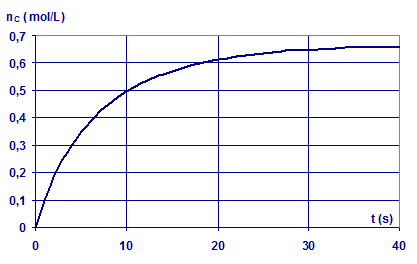 |
n0A = 1
mol/L
n0B = 1 mol/L
k1 = 0,1 L/mol/s
k2 = 0,025 L/mol/s
K = k1/k2 =
4
nCmax = K1/2/(K1/2 + 1)
n0B
= 0,667 mol/L |
Caso particular:
n0A
>> n0B portanto
k1 (n0A + n0B) nC
>> (k1 - k2) nC²
dnC/dt + k1 (n0A + n0B)
nC - (k1 - k2) nC²
= k1 n0A n0B passa a:
dnC/dt + k1
n0A nC = k1 n0A
n0B
A solução é:
nC = n0B
(1 - exp(- k1 n0A t ))
A constante de tempo τ = 1/(k1 n0A)
(A t = τ, nC = 63% de nCmax
)
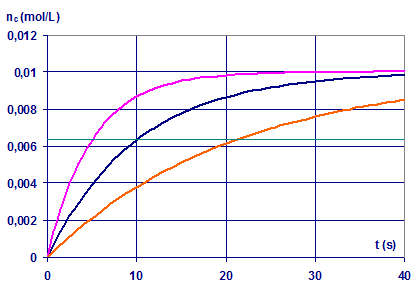 |
n0A = 1
mol/L
n0B = 0,01 mol/L
ΔA = 52 kJ/mol
nCmax = 0,01 mol/L
A 25°C k1
= 0,1 L/mol/s
τ = 1/(k1 n0A)
= 10 s (A t = 10 s, nC = 0,0063
mol/L)
A 15°C k1
= 0,0474 L/mol/s τ = 21 s
A 35°C k1
= 0,201 L/mol/s τ = 5 s |
|

![]()