|
Constante de Boltzmann k = 1,380 650 3 × 10-23 J/K
Constante de Planck h = 6,626 068 74 × 10-34 J.s
Velocidade da luz c = 299 792 458 m/s
1. Probabilidade de troca átomo-fotão
O fotão é um bosão, segue portanto a estatística de Bose-Einstein.
A probabilidade de emissão de um bosão na presença de n bosões idênticos é proporcional a n+1 [Pe = (n+1) p]
e a probabilidade de absorção é proporcional a n [Pa = n p] (p: probabilidade de emissão do bosão sozinho).
*
2. Equilíbrio térmico do corpo negro
O corpo negro é constituído por uma cavidade oca com volume V à temperatura
T, em equilíbrio térmico. Os átomos da parede absorvem os fotões presentes na cavidade e depois reemitem-nos. Oscilam portanto
entre dois níveis de energia Ea e Ee, separados por ΔE = hν
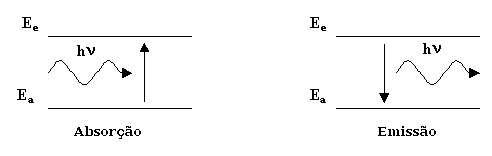
Ne átomos estão no estado Ee e Na no estado Ea. A cavidade contém n fotões.
O número de fotões emitidos é portanto Ne Pe = Ne (n+1) p
e o número de fotões absorvidos é Na Pa = Na n p
Em equilíbrio térmico, estes dois valores são iguais, logo Ne (n+1) p = Na n p ou
Ne (n+1) = Na n
Ora, em equilíbrio térmico, também Ne/Na = e -ΔE/kT (fórmula de Boltzmann),
logo: n/(n+1) = e -ΔE/kT e, portanto: n = 1/(e ΔE/kT -1) = 1/(e hν/kT -1)
A energia dos fotões de frequência ν é então Eν = n hν = hν/(e hν/kT -1)
3. Número de modos contidos no intervalo de frequência
δν
Num comprimento L, há uma onda estacionária de polarização dada se
L = j λ /2 ou L = j π/kj, logo: kj = j π/L (j inteiro).
O intervalo entre dois números de onda sucessivos é então δk = π/L.
O número de valores de k compreendidos dentro de um intervalo δk >> δk é então
δk /δk = δk L/ π
Porém, numa onda estacionária contendo duas ondas, o número de modos δM não é mais que a média do número de valores de
k, logo: δM = δk L/ 2π
A 3 dimensões, δM = δMx δMy δMz =
δkx Lx/2π δky Ly/2π
δkz Lz/2π = LxLyLz/(2π)3
δkx δky
δkz
δM = V /(2π)3
δk3. Tendo o fotão dois estados de polarização possíveis,
δM = 2V/(2π)3δk 3
δk3 é o intervalo de volume esférico no
espaço dos k e vale portanto 4πk² δk.
Logo: δM = 8πV/(2π)3
k2δk = V/π2 k 2δk.
k = 2πν/c logo: δM = 8πVν2/c3 δν
4. Energia volúmica do corpo negro
A cavidade contém δM modos, contendo cada um a energia
Eν = hν/(e hν/kT -1) em cada intervalo de frequência δν
A energia contida no intervalo de frequência δν é então δE = 8
πVν2/c3 hν/(e hν/kT -1)
δν
dE = 8πVhν3/ (c3(e hν/kT -1) )
δν
Energia volúmica por intervalo de frequência dν: dE = δ
E/V
dE = 8πhν3/
(c3 (e hν/kT -1) ) dν
Energia volúmica por intervalo de pulso
dω
ν = ω/2π logo:
dν = dω/2π.
Tem-se então dE = 16π2 hω
3/(c3 (e hw/kT -1) )
dω/16π4 = hω
3/(π2c3 (e hw/kT -1) )
dω com h = h/2π
dE =
hω3/(π2c
3 (e hw/kT -1) )dω
Energia volúmica por intervalo de
comprimento de onda dλ
λ = c/ν ou ν = c/λ logo: dν = (-)
c/l2 dλ. Tem-se então dE = 8π hc3/(λ3
c3 (e hc/kλT -1) ) c/λ2 dλ .
dE = 8π
hc/(λ5(e hc/kλT -1) )dλ
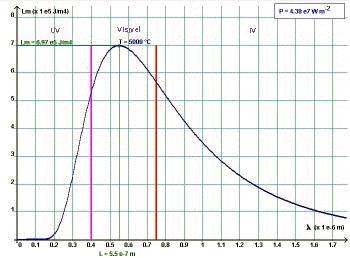
Lei de emissão do corpo negro (Lei de Planck)
|
Energia volúmica por
intervalo de comprimento de onda
|
Curva dE/dλ = f (λ)
 |
|
dE
8πhc
1
--- = ---- ------------
dλ
λ5
( e hc/kλT
- 1 )
|
5. Lei de Wien
A curva passa por um valor máximo quando λ5 (
e hc/kλT - 1 ) passa por um valor mínimo.
Derivando em relação a λ: 5λ4(
e hc/kλT - 1 ) - λ5 hc/(kλ2T
)e hc/kλT = 0
Simplificando: λ4 : 5 ( e hc/kλT
- 1 ) - hc/(kλT ) e hc/kλT
= 0 logo: ( 5 - hc/(kλT )) e hc/kλT - 5 = 0
Considera-se hc/(kλT) = u
( 5 - u ) e u - 5 = 0
Considera-se 5 - u = x
então: x e 5-x = 5 logo: x e 5 e -x = 5 e, deste modo: e
5/5 x = e x
Resta resolver esta equação, o que não é muito evidente de não for feito numericamente.
.
A solução é o ponto de coincidência inferior das curvas
y = e 5/5 x e y = e x
que é aproximadamente y = 30 x e y = e x . Manifestamente, y
é próximo de 1 e portanto x é próximo de 1/30.
Como x << 1, pode-se desenvolver e x na série de Taylor em 2a
ordem: e x = 1 + x + x2/2
Logo: 1 + x + x2/2 = e 5/5 x
x2 - 2( e 5/5 -1 ) x + 2 = 0
A solução é então: x = ( e 5/5 -1 ) - ( ( e 5/5 -1)
2 - 2 ) 1/2 = 0,03488552 (A determinação
numérica dá 0,0348857682557236963, logo a aproximação é muito boa).
u = hc/(kλT) = 5 - x = 4,9651142317442763037
λ = hc/( 4,9651142317442763037 kT ) = 2,8977686 × 10-3/T , é a Lei do
deslocamento de Wien.
Lei de Wien
6. Intensidade luminosa em função da frequência
A intensidade luminosa I é a potência luminosa por m² à frequência ν
no interior do corpo negro.
É a energia produzida num segundo à frequência ν numa secção de 1 m², é portanto a energia contida num volume
de secção 1 m² e de comprimento c: V = c
É portanto: I (ν) = V dE/ dν = c dE/ dν = 8πhν3 /
(c2(e hν/kT -1)) ou
I (ω) = c dE/dω = hω3/(π
2c2 (e hω/kT -1) )
I (ν) = 8π
hν3/(c2(e hν/kT -1))
ou
I (ω) = hω3/(π
2c2(e hω/kT -1))
7. Lei de Stefan-Boltzmann
A lei de Stefan-Boltzmann (ou lei de Stefan) dá a potência luminosa que sai
de um corpo negro por uma superfície de 1 m².
Esta energia é o quarto da energia à frequência ν contida num volume V de secção 1 m² e de comprimento c.1s : V = c.
É então um quarto da intensidade luminosa à frequência ν.
Porquê um quarto? Porque metade da luz volta para trás e a luz que vem para a frente propaga-se em todas as
direções, e tem portanto um fator cosseno que leva de novo a um fator de 1/2.
É então o integral em todos os ν da função I(ν)/4 = 2πhν3/
(c2(e hν/kT -1))
| P = |
 |
I(ν)/4 dν = |
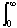 |
2πhν3/(c2(e hν/kT -1)) dν |
Considera-se u = hν/kT, tem-se então I dν
= 2πh(kTu/h)3/c2 / (eu -1) kT/h du
= 2πk4T 4/h3/c2
u3/(eu -1) du
|
logo: P = 2πk4T4/h 3
/c2 |
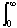 |
u3/(eu -1)du
pois |
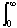 |
u3/(eu -1) du =
π4/15, ** |
logo: P = 2π5k4/
(15 h3c2) T4 = σT4 (Lei de Stefan)
A constante de Stefan-Boltzmann: σ = 2π5k4
/(15 h3c2) = 5,6703994 × 10-8 W m-2
K-4
Lei de Stefan-Boltzmann
|
P = σ T4
s = 5,67040 × 10
-8 W m-2 K-4 |
8. Exemplos de aplicações
8.1 Determinação do albedo terrestre
O albedo é a proporção de energia luminosa solar que não é absorvida pela
Terra, é refletida pela atmosfera.
Dados e medidas possíveis a partir da Terra:
RT: raio da Terra
RS: raio do Sol
d: distância Terra-Sol
θ: diâmetro aparente do Sol = 2RS/d = 32'
= 9,308 × 10-3 rd
TT: Temperatura média da atmosfera terrestre = -18 °C = 255 K
(Viva o efeito de estufa!!!)
TS: Temperatura da superfície do Sol
lmax do Sol = 0,5014 µm
TS = 2,898 × 10-6/λmax
= 5780K (Aplicação da Lei de Wien)
Potência emitida pelo Sol P0 = 4πRS2σ TS4
(Aplicação da Lei de Stefan)
Potência recebida pela Terra PS = P0 πRT2/4πd2
= P0 RT2/4d2 = 4πRS2σ
TS4RT2/4d2 = πθ2σ
TS4RT2/4
Potência emitida pela Terra PT = 4πRT2σ TT4
(Aplicação da Lei de Stefan)
PT/PS = 4πRT2σ TT4 /
(πθ2σ TS4RT2/4) = 16/θ2
( TT/TS )4 = 0,689
Albedo a = 1- PT/PS = 0,311 (Cerca de 30 % da
energia recebida é refletida pela atmosfera.)
8.2 Determinação da perda de massa do Sol
Dados:
RS: raio do Sol = 696265 km
TS: Temperatura da superfície do Sol = 5780K
Potência emitida pelo Sol PS = 4πRS2
σ TS4 = 3,85 × 1026 W
Massa perdida por segundo (relação de Einstein) = PS/c2
= 4,291 × 109 kg/s (mais de 4 milhões de toneladas por segundo!!)
Por outro lado, o Sol perde também cerca de 1 milhão de toneladas de matéria por segundo devido ao vento solar.
Massa perdida pelo Sol depois da sua formação (4,6 109 anos):
M = 5,3 × 109x 4,6 × 109 x 365,25 x 24 x 3600 = 7,7 × 1026 kg
(cerca de 128 massas terrestres, o que é muito pouco (0,038%) em relação à massa do Sol que é igual a
333432 massas terrestres.
Cálculo do integral de u3/
(eu -1)du
Sabendo que Σ qn
= q/(1 - q ) = 1/( 1/q -1 ), tem-se 1/(eu -1) = 1/(1/e-u -1) = Σ
(e-u)n = Σ
e-nu logo:
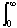 |
u3/(eu -1)du é igual a |
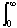
|
Σ ( u3e-nu )du
= Σ |
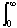 |
u3e-nu du
|
Integrando três vezes por partes, tem-se então:
| Σ |
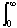 |
3u2 e-nu /n du, depois
Σ
|
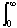 |
-6u e-nu /n2 du,
depois Σ |
 |
6 e-nu /n3 du
que vale Σ
6/n4 = 6Σ 1
/n4 |
| então
Σ 1/n4 = π
4 /90, logo: |
 |
u3/(eu -1) du = π
4 /15 |
*
Os puristas poderão inquietar-se pelo facto de uma probabilidade poder claramente
ultrapassar 1! Será necessário normalizá-la. Na prática, não há lugar para essa preocupação dado que apenas se utilizam
as razões das probabilidades.
Traduzido e adaptado
para a Casa das Ciências por Diana Barbosa e Manuel Silva Pinto em outubro de 2011

|