Constante de Boltzmann      k = 1,380 650 3 × 10^-23 J/K
Constante de Planck            h = 6,626 068 74 × 10^-34 J.s
Velocidade da luz                  c = 299 792 458 m/s

1. Transições energéticas nos átomos

1.1 Níveis de energia nos átomos

A energia dos átomos é quantificada, não pode tomar um valor arbitrário. Os valores permitidos são chamados de níveis de energia do átomo. Os eletrões preenchem esses níveis de energia e o último nível ocupado por, pelo menos, um eletrão é o nível fundamental. Os níveis superiores são chamados de níveis excitados.

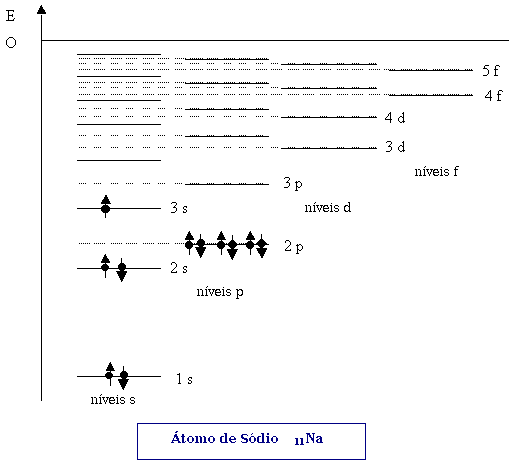O esquema ao lado esquerdo representa os 20 primeiros níveis de energia do átomo de Sódio, sem ter em consideração a escala. Cada nível contém subníveis que podem conter, cada um, 2 e- de spin oposto.          s ( L = 1 ) : 1 subnível : 2e-          p ( L = 2 ) : 3 subníveis : 6e-          d ( L = 3 ) : 5 subníveis : 10e-          f ( L = 4 ) : 7 subníveis : 14e-          n ( L = n ) : (2n-1) subníveis : (4n-2)e- Os eletrões de sódio ocupam os níveis:      1s ( 2e- ), 2s ( 2e- ), 2p ( 6e- ) e 3s ( 1e- ) O nível fundamental do sódio é o nível 3 s. A "famosa" risca amarelo-alaranjada do sódio a 589 nm, que é usada para iluminar rotas nos nossos túneis é devida à transição de 3p para 3s ( 2,105 eV ).

1.2 Emissão e absorção de um fotão por um átomo

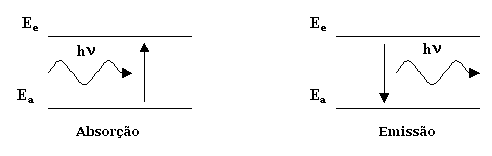
Um fotão que tenha uma energia hν igual à diferença entre a energia do nível fundamental E_f e a de um nível excitado E_n, pode ser absorvido, o que conduz o átomo à energia E_n. Diz-se que está então num estado excitado.

Condição de absorção de um fotão:
hν = hc/λ = E_n - E_f
λ = hc/(E_n - E_f )

O átomo excitado num estado E_n não se vai manter muito tempo nesse estado, voltará a um estado inferior E_m, emitindo um fotão de energia hν igual à diferença entre a energia E_n e a energia E_m. Se o estado E_m não é o nível fundamental, ele vai descer de novo a um estado inferior, emitindo um novo fotão e assim sucessivamente, em cascata, até ao estado E_f.

Comprimento de onda do fotão emitido durante uma transição:
hν = hc/λ = E_n - E_m
λ = hc/(E_n - E_m )

Nota: Os níveis de energia do átomo não são somente caracterizados pela sua energia, mas têm também um momento cinético que é, ele próprio, quantificável e que pode ser caracterizado por um número inteiro L.
O fotão tem também um momento cinético, o seu spin, que vale 1 ou -1. Logo, para conservar o momento cinético, é necessário que a transição se faça entre dois níveis em que os L sejam diferentes de 1. Há então transições "interditas" entre certos níveis.

2. O Laser

2.1 Emissão estimulada

Ao estudar o resultado de Planck que davam a intensidade da luz emitida por um corpo negro   [ I (ν) = 8πhν³/(c²(e ^hν/kT -1)) ], que ele tinha encontrado ao conjeturar que a energia dos átomos era quantificável, Einstein descobre que se pode também chegar a esse resultado ao supor que a energia da luz é também ela quantificável sob a forma de fotões de energia hν (o que lhe permitiu, por outro lado, explicar o efeito fotoelétrico que lhe valeu o Prémio Nobel) e que a probabilidade de transição de um átomo entre dois níveis é proporcional ao número de fotões com boa energia, presentes na cavidade de um corpo negro. Esta conjetura faz sentido para a transição a um nível superior, quantos mais fotões houver, maior é a possibilidade que um deles seja absorvido. O que está longe de ser óbvio, é que isto é igualmente verdadeiro para a desexcitação do átomo, que parece, a priori, um fenómeno totalmente independente da presença ou não de fotões nas proximidades.

Vejamos o raciocínio de Einstein:
Estudemos o equilíbrio de um corpo negro que contenha átomos de níveis E_f e E_n separados pela energia ΔE, que absorvem e emitem fotões de energia hν = ΔE. Em equilíbrio, são tantos os átomos que absorvem fotões de energia hν como os que a emitem.
N_f átomos estão no estado E_f e N_n átomos estão no estado E_n. Segundo Boltzmann, N_n/N_f  =  e ^-ΔE/kT
A probabilidade de um átomo estar excitado no segundo seguinte é proporcional ao número de fotões de energia hν = ΔE. Ora, I (ν) é precisamente proporcional a este número, logo esta probabilidade pode ser notada p = P_fn I(ν) e o número de átomos que vão passar ao estado n em cada segundo é então:
                                                                                                                                                         N_fn = N_f P_fn I(ν)
A probabilidade de um átomo emitir um fotão de energia hν = ΔE, para voltar ao estado f, decompõe-se em dois termos. Uma probabilidade P_s, que é a probabilidade de transição espontânea que terá lugar sem a presença de fotões na proximidade, e uma probabilidade P_nf I(ν), devida à presença de fotões (é a probabilidade de emissão "estimulada" pela presença de fotões). Logo, o número de átomos que vai passar ao estado f a cada segundo será:
                                                              N_nf = N_n ( Ps + P_nf I (ν))
Em equilíbrio, N_fn = N_nf, logo:
                                                N_f P_fn I(ν) = N_n ( P_s + P_nf I(ν))    logo:   N_n/ N_f  = e ^-ΔE/kT = P_fn I(ν) / ( P_s + P_nf I(ν))
                                      logo:   P_s e^-ΔE/kT + P_nf I(ν) e ^-ΔE/kT = P_fn I(ν)   logo:   I(ν)  = P_s e ^-ΔE/kT/ ( P_fn - P_nf e ^-ΔE/kT )
Dividindo numerador e denominador por e^-ΔE/kT, obtém-se:   I(ν) = P_s/( P_fne ^ΔE/kT - P_nf ),    ΔE = hν   logo, obtém-se:    I(ν) = P_s/( P_fne ^hν/kT - P_nf ).
Se se comparar esta relação com a de Planck:   I(ν) = 8π hν³/c²/(e ^hν/kT -1)), vê-se que têm a mesma expressão se   P_fn = P_nf        (Entre dois níveis, a probabilidade de emissão estimulada é igual à probabilidade de absorção de um fotão.)
E se P_s/P_fn = 8πhν³/c²,   tem-se então   I(ν) = P_s/P_fn/( e ^hν/kT  - 1 ) = 8πhν³/c²/ ( e ^hν/kT  - 1 ),   o que é o resultado de Planck e que valida a existência da emissão estimulada.

Nota: Uma teoria mais recente recorre à natureza de bosão do fotão, onde a probabilidade de ser absorvido é proporcional ao número n de bosões idênticos já presentes e a probabilidade de ser emitido é proporcional a n+1. É devido ao facto da probabilidade de emitir um bosão idêntico (mesma energia, mesmo spin e mesma quantidade de movimento, logo, mesma direção) aumentar enormemente com o número n, que o Laser emite uma luz coerente (fotões idênticos). Este aspeto não foi mencionado na teoria acima apresentada.

2.2 Princípio do Laser

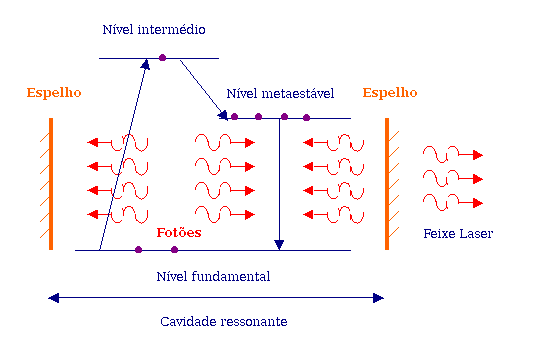
A existência de emissão estimulada permitiu a tornar realidade uma fonte de luz muito potente e muito direcional, o Laser.
Um conjunto de átomos é mantido num estado excitado por uma fonte de energia exterior (uma lâmpada potente ou uma corrente elétrica que preenche um nível metaestável, passando por um nível intermédio superior). Escolhe-se um estado metaestável ou a probabilidade de desexcitação espontânea é a mais baixa possível. Certos átomos desexcitam-se e os fotões emitidos podem induzir a transição de outros átomos, produzindo então um fotão idêntico que pode, por sua vez, provocar uma nova transição de um outro átomo. Tem-se um efeito "bola de neve" e pode-se obter rapidamente um grande número de fotões idênticos. Se se alcança manter os átomos no seu estado excitado "bombeando" permanentemente os e^-, pode-se ter uma produção contínua de luz coerente. Este é o princípio mas, na verdade, os fotões, uma vez emitidos, ficam muito pouco tempo no meio ativo e têm então poucas possibilidades de induzir uma emissão estimulada. Daí a ideia de os manter encerrados no meio, colocando dois espelhos extremamente refletores nas duas extremidades da cavidade que contém os átomos ativos. Assim, os fotões passam e voltam a passar um grande número de vezes, o que aumenta a sua possibilidade de provocar uma emissão estimulada e, deste modo, a cavidade encontra-se rapidamente cheia de fotões idênticos que acabam por atravessar um dos espelhos, originando um feixe retilíneo de luz monocromática coerente.
A emissão espontânea perturba o fenómeno pois sendo Ps/P_fn proporcional a ν³, esta emissão espontânea é ainda mais importante que a frequência da luz emitida ser elevada. É por isso que os primeiros Lasers estavam feitos com Masers emitindo em micro-ondas. Os Lasers mais potentes são ainda os de infravermelhos e é muito difícil produzir um Laser UV. Quanto ao Laser X, está ainda em estado de projeto longínquo.

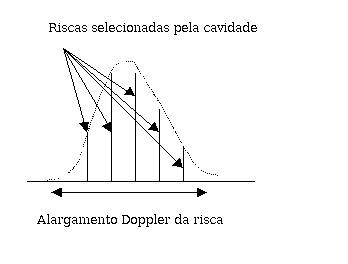
2.3 Monocromatismo do Laser

Os fotões emitidos pelos átomos excitados não são todos perfeitamente idênticos, há uma certa dispersão de frequência devida ao efeito Doppler (por causa da agitação térmica, para os gases, e das interações com os átomos vizinhos, para os sólidos). Existe também o princípio da incerteza de Heisenberg, que liga a incerteza sobre a frequência ao tempo de permanência do eletrão no nível excitado, mas é um efeito muito inferior ao anterior. Tem-se então um conjunto contínuo de frequências, centrado na frequência teórica, e a risca é dilatada. Estando a cavidade de largura L fechada por dois espelhos, as ondas refletidas interferem com as ondas incidentes e tem-se um fenómeno de ressonância, em que só subsistem os comprimentos de onda tais que   L = kλ/2  Logo:   λ = 2L/k  ( k inteiro ) Sendo L muito superior a λ, k é muito elevado e a diferença entre dois λ e λ' sucessivos é muito pequena:   λ = 2L/k   e   λ' = 2L/(k+1) Δλ = λ - λ' = 2L(1/k -1/(k+1)) = 2L(1/(k(k+1))) = 2L/k²  ( k>>1 ) Ora,   k = 2L/λ   logo:   Δλ = λ²/2L e       Δλ/ λ = λ/2L    (Ex.: Para λ = 6.10-7m e L = 0,3 m , obtém-se Δλ = 6.10-13 m. A largura da risca emitida em λ é geralmente próxima a 2,5.10-12 m e tem-se então cerca de 4 ou 5 riscas muito próximas que são emitidas pelo Laser. Assim, ele não é estritamente monocromático mas, em contrapartida, graças à ressonância da cavidade, as riscas são muito finas)

 
    Traduzido e adaptado para a Casa das Ciências por Diana Barbosa e Manuel Silva Pinto em outubro de 2011