|
1. A refração

Lei de Descartes : n1
sen i = n2 sen r (cf: refração)
2. As lentes delgadas nas condições de Gauss
2.1 Diagrama do dioptro
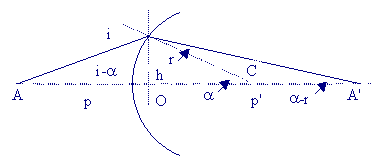 |
p = OA
( p < 0 )
p' = OA'
( p' > 0 )
R = OC ( R
> 0 ) |
2.2 Relação do dioptro
sen α
= h/R
n1 sen i = n2 sen r
tan ( i -α ) = - h/p ( p < 0 )
tan ( α - r ) = h/p'
Aproximações de Gauss: os ângulos são pequenos, portanto h é
pequeno e O está muito próximo do dioptro (raios paraxiais).
Na prática, impõe-se que h<R/10
Tem-se portanto: sen ε
= tan ε = ε
logo:
α = h/R
n1 i = n2 r
i - α = - h/p
α - r = h/p'
logo:
i = α - h/p
= h/R - h/p
r = α - h/p' = h/R - h/p'
n1 i = n2 r
= n1 ( h/R - h/p ) = n2
( h/R - h/p' )
logo: n2 h/p' - n1
h/p= ( n2 - n1 )h/R
logo:
n2 /p' - n1/p = ( n2 - n1 ) /R
Relação de combinação dos dioptros.
A relação não depende de h, portanto todos os raios que partem de A
convergem em A'. Nas condições de Gauss, o dioptro é, portanto, estigmático.
2.3 Relação das lentes delgadas

Lente delgada: O está muito próximo das superfícies dos dois dioptros.
Ar: índice = 1
Lente: índice = n
1º dioptro (n1 = 1, n2 = n):
n /p1
= ( n -1) /R1 + 1/p
(R1 > 0)
2º dioptro (n1 = n, n2 = 1):
1 /p'
= (1 - n ) / R2 +
n/p1 (R2 < 0)
logo: 1/p' = ( n - 1 ) /R1
- ( n - 1 ) /R2 + 1 /p
1/p' - 1 /p = ( n - 1 )( 1 /R1
- 1 /R2 ) = 1/f ' =
C Lei de Descartes para as lentes delgadas
2.4 Distância focal
A distância focal f ' = OF ' é a distância entre o centro da lente
e o local onde se forma a imagem de um objeto colocado no infinito.
Se p é infinito, 1 /p' = ( n - 1 )( 1 /R1
- 1 /R2 ) = 1/f ' =
C
1/f ' = C = ( n - 1 )(
1 /R1 - 1
/R2 )
Lentes convexas: R1 >
0 e R2 < 0 ou 1/R1 >
1/R2, logo: f ' > 0
e C = 1/f ' > 0 (F ' à direita do espelho)
Lentes côncavas: R1 < 0 e R2 >
0 ou
1 /R1 < 1
/R2, logo: f ' < 0 et C = 1/f ' < 0
(F ' à esquerda do espelho)
2.5. As lentes esféricas fora das condições de Gauss
Estudo da distância focal f = OF de uma lente plano-convexa:
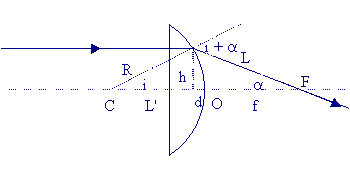 |
f0 =
(n-1)R
OF = f
L' = R cos i = ( R² - h²)1/2
d = R - L' = R - ( R² - h²)1/2
f ' = f + d = L cos α
f ' = f + R - ( R² - h²)1/2
L = ( f '² + h² )1/2
|
n sen i = sen( i + α ) = sen i cos α + senα
cos i
n = cosα + senα/tan
i = f '/L + h/L L'/h = f '/L + L'/L = ( f ' + L' )/L
L = ( f ' + L' )/n logo: L² = ( f '² + L'² + 2 f 'L'
)/n² logo: f '² + h² = ( f '² + L'² + 2 f 'L' )/n²
( n² -1 ) f '² + 2 f 'L' + n²h² - L'² = 0
f ' = ( L' + ( L'² - ( n² -1 ) ( n²h² - L'² ))1/2 )/( n² -1 )
(O outro sinal não tem sentido físico)
f ' =
( L' + ( L'² - n4h² + n²L'² - L'² + n²h² )1/2)/(
n² -1 )
f ' = ( L' + ( - n4h² + n²L'² + n²h² )1/2)/( n² -1 )
= ( L' + n ( R² - n²h² )1/2)/( n² -1 ) = ( ( R² - h²)1/2 +
n ( R² - n²h² )1/2)/( n² -1 )
f + R - ( R² - h²)1/2 = ((R² - h²)1/2 + n ( R²
- n²h² )1/2)/( n² -1 )
f = ((R² - h²)1/2 + n ( R² - n²h² )1/2)/( n²
-1 ) - R + ( R² - h²)1/2 = ( n²(R² - h²)1/2 +
n ( R² - n²h² )1/2)/( n² -1 ) - R
f = R (n( n(1 - h²/R²)1/2 + (1 - n²h²/R²)1/2)/(
n² -1 ) - 1)
f = f0 (n( n(1 - h²/R²)1/2 + (1 - n²h²/R² )1/2)/(
n + 1 ) - n + 1) ( f0
= R/(n-1) é a distância focal da lente)
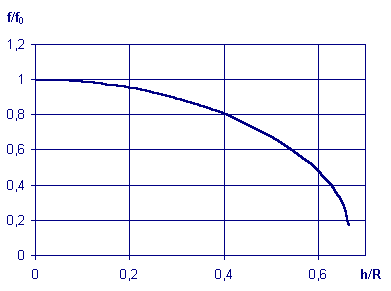 |
Curva f/f0 = f(h/R) para n = 1,5
f0 = R/(n-1)
f é independente de h para h < 0,1R
Para h/R = 1/n = 0,667, fm = 0,171 f0
|
Valor limite de f
f não existe a não ser que R² - n²h² >= 0, logo, se h/R <= 1/n ou sen i <= 1/n
sen i = 1/n corresponde ao ângulo limite de saída do raio da lente, onde i + α = 90°
Se h/R = 1/n, tem-se então fm = R( n²(1 - 1/n²)1/2 )/( n² -1 ) - R = R n/( n² -1 )1/2
- R
fm = R ( n/( n² -1 )1/2 - 1 ) = f0 ( n(n-1)1/2/(n+1)1/2
- n + 1 )
( f0 = R/(n-1) é a distância focal da lente)
Valor de f para os valores baixos de h (h²/R² << 1)
f = ( n²(R² - h²)1/2 +
n ( R² - n²h² )1/2)/( n² -1 ) - R = ( n²R(1 - h²/R²)1/2
+ nR( 1 - n²h²/R² )1/2)/( n² -1 ) - R
f = ( n²R(1 - h²/2R² ) + nR( 1 - n²h²/2R² ))/( n²
-1 ) - R = ( n²R - n²h²/2R + nR - n3h²/2R)/( n² -1 ) -
R
f = (n²R + nR - n²( n + 1)h²/2R - n²R + R )/( n² -1 ) = ( n + 1
)R/( n² -1 ) - n²( n + 1)h²/2R /( n² -1 ) = R/( n -1 ) - n²h²/2R /( n -1
)
f = R/( n -1 ) ( 1 - n²h²/2R²) = f0 ( 1 -
n²h²/2R²)
( f0 = R/(n-1) é a distância focal da lente)
Para que f seja superior a 99% de f0
(Condições de Gauss), é necessário que n²h²/2R² < 0,01, logo: h²/R² < 0,02/n² = 0,01,
logo: h/R < 0,1.
Está-se dentro das condições de Gauss se o raio da zona útil (do diafragma) é inferior a R/10 ou se o
diâmetro é inferior a f0/10.
3. Os espelhos esféricos nas condições de Gauss
3.1 Diagrama do espelho
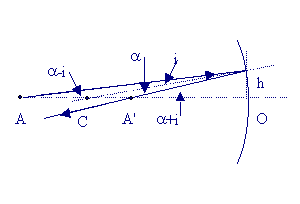 |
p = OA
(p < 0)
p' = OA'
(p' < 0)
R = OC (R < 0)
|
3.2 Relação dos espelhos esféricos
sen α = - h/R (R < 0)
tan (α - i ) = - h/p (p < 0)
tan (α + i ) = - h/p' (p' < 0)
Aproximações de Gauss: os ângulos são pequenos, logo h é pequeno e
O está muito próximo da superfície do espelho (raios paraxiais).
Na prática, impõe-se que h<R/10.
Tem-se portanto: sen ε = tan ε = ε
logo:
α = - h/R
α - i = - h/p
α + i = - h/p'
logo:
2 α = - h/p - h/p' = - 2 h/R
logo:
1/p' +
1 /p = 2 /R = 1/f ' =
C
Lei de Descartes para os espelhos esféricos
A relação não depende de h, portanto todos os raios que partem de A
convergem em A'. Nas condições de Gauss o espelho é, portanto, estigmático.
3.3 Distância focal
A distância focal f ' = OF ' é a distância entre o centro do espelho e o local onde se forma a imagem
de um objeto colocado no infinito.
Se p é infinito, 1 /p' = 2/R = 1/f ' =
C
OF ' = f ' =
1/C = R/2
Espelho côncavo: R < 0,
logo: C < 0 (F ' à esquerda do espelho)
Lente convexa: R > 0 logo: C > 0 (F ' à direita do espelho)
3.4 Os espelhos esféricos fora das condições de Gauss
Estudo da distância focal f = OF de uma lente plano-convexa:
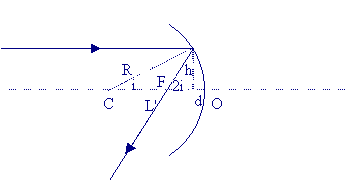 |
OF = f
L' = R cos i = ( R² - h²)1/2
d = R - L' = R - ( R² - h²)1/2
f ' = f - d
f ' = f - R + ( R² - h²)1/2 |
f ' = h/tan 2i = h cos 2i/sen 2i = h
cos 2i/( 2 sen i cos i ) = h f '/(f '² + h² )1/2 /( 2 h/R L'/R
)
h/(f '² + h² )1/2 = 2 hL'/R²
(f '² + h² )1/2 = R²/(2L') logo: L' = R²/(2 (f '² + h² )1/2)
L'² = R4/(4 (f '² + h² )) e L'² = ( R² - h² )
R² - h² = R4/(4 (f '² + h² )) logo: f '² + h²
= R4/(4(R² - h²)) = R²/(4(1 - h²/R²))
f '² = R²(1/(4(1 - h²/R²)) - h²/R²) = R²(1 - 4 h²/R²(1
- h²/R²)/(4(1 - h²/R²)) = R²(1 - 2h²/R²)²/(4(1 - h²/R²))
f ' = R(1 - 2h²/R²)/(2(1 - h²/R²)1/2)
(O outro sinal não tem sentido físico)
Por outra parte, f ' = f - R + ( R² - h²)1/2 logo:
f = R(1 - 2h²/R²)/(2(1 - h²/R²)1/2) + R - (R² - h²)1/2
= R (1 - (1 - h²/R²)1/2 + (1 - 2h²/R²)/(2(1
- h²/R²)1/2))
f = R(2(1 - h²/R²)1/2 - 1)/(2(1 - h²/R²)1/2
) = R(1 - 1/(2(1 - h²/R²)1/2 ))
f = R(1 - 0,5/(1 - h²/R²)1/2) = f0 (2 - 1/(1 - h²/R²)1/2)
(f0 = R/2 é a distância focal do espelho)
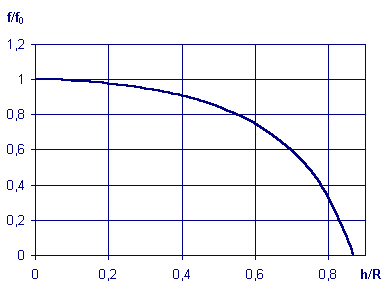 |
f0 = R/2
f é independente de h para h < 0,15 R
Para h/R = sen 60° = 0,866, f = 0
|
Valor de f para os baixos valores de h (h²/R² << 1)
f = R(1 - 1/(2(1 - h²/R²)1/2 ))
f = R(1 - (1 + h²/2R²)/2) = R(1/2 - h²/R²/4))
f = 0,5 R(1 - h²/2R²) = f0 (1 -
h²/2R²) (f0 = R/2 é a distância focal do espelho)
Para que f seja superior a 99% de f0 (Condições de Gauss),
é necessário que h²/2R² < 0,01, logo: h²/R² < 0,02, logo: h/R < 0,14.
Está-se dentro das condições de Gauss se o raio da zona útil (do diafragma) é inferior a R/10 ou se o
diâmetro é inferior a 4f0/10, próximo de f0/2.
Para um telescópio com distância focal de 1m, isto corresponde a um espelho com 40 cm de diâmetro. Obtém-se então
uma imagem de um ponto que consiste num halo fino de 2 mm de raio. Não é muito aparente, mas é inaceitável para
imagens de alta resolução. É por isso que nos telescópios astronómicos se utilizam espelhos parabólicos que
são perfeitamente estigmáticos.
4.
Poder de resolução de um
instrumento ótico
Traduzido e adaptado
para a Casa das Ciências por Diana Barbosa e Manuel Silva Pinto em Setembro de 2011

|